大数的认识

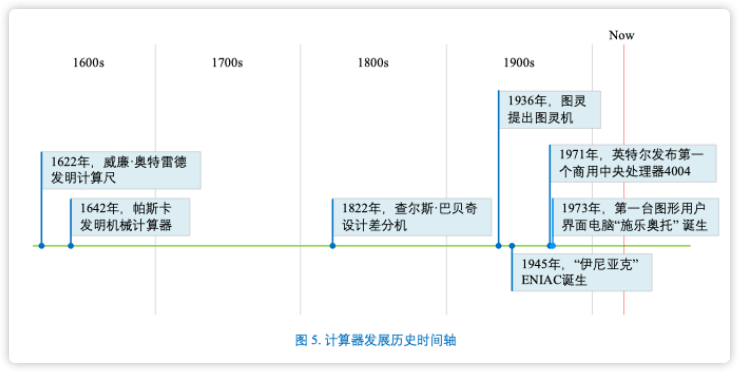
计算器发展时间轴

“拖数游戏”：305005

秦静钊.从困惑中寻找对策——以《大数的认识》的教学为例[J].广西教育,2015(37):23-24.

向前拖动，数字变成了3050050，观察“0”的位置有什么变化，又该怎么读？学生懂得了第一个“0”在万级中间，要读，个级前面两个“0”只读一个，末尾的“0”不读。

向前移动，数字变成了30500500，再观察“0”的位置有什么变化，又该怎么读？学生得出：万级第一个“0”在中间，要读，第二个“0”在末尾，不读；个级第一个“0”在前面，要读，后两个“0”在末尾，不读。

通过三个数的比较，学生发现“0”在不同位置，就有不同的读法，从而归纳出“0”的读法规律：每级中间的“0”不管有几个，只读一个“0”，每级末尾的“0”不读。

计数体系分析

刘加霞,孙庆辉.熟悉而又陌生的“十万”——解读“大数的认识”教学难点[J].小学教学(数学版),2010(01):22-23.

四位一分级是学生正确读数与写数的基础，因为汉语读数的计数法与书写数的“十进位值制”计数法从属于两种不同的计数体系。汉语读数属于乘法分群系统，即从高到低（最小计数单位“一”或“个”省略）直接将计数单位的个数与计数单位连续地说出或写出，例如5625就读做“五千六百二十五”，也就是“五乘一千加六乘一百加二乘十加五乘一”。在乘法分群系统中就会出现一个数的中间或者末尾有几个零省略不读的情况，即不用“0”来“占位”，这就增加了学生读、写大数的难度。

单元复习课

张家萍.突破难点 串珠成链——“大数的认识”单元复习教学研课与反思[J].小学教学参考,2021(20):70-71.

两条数学信息：（1）某银行第二季度的欧元存款正好是98600000元。（2）某企业今年的电子商务销售额约98600000元。然后以“这两条信息中的98600000元一样吗？”这一问题驱动学生自主复习，并设计如下教学引导：（1）想一想：这两条信息中的98600000元有什么不同点？（2）画一画：请你在数线上表示两个98600000的不同点。

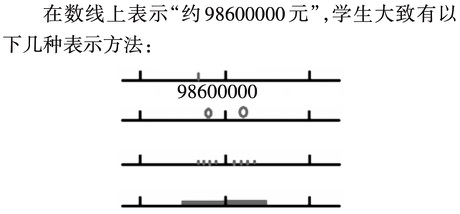
小结准确数和近似数的不同点：准确数是数线上的一个点，近似数是数线上的一个区域。

请 Ta 喝咖啡 ☕️

喝咖啡记录：